Аппаратно независимые математические модели цвета
Аппаратно независимые
математические цветовые
модели - необходимость при работе с
цветом в цифровом виде, исследования
природы цвета идут с незапамятных времен,
но только в последнее время эта наука
перешла из теоретической физики в
прикладную область. Рассмотрим, к примеру:
аппаратно независимую модель (HSB), где каждый цвет
описан
тремя основными значениями:
- тон (hue)
- насыщенность (chroma)
- яркость (Brighness)

Эти три стакана
ясно показывают,
что эти термины описывают. На левой иллюстрации
расположены по кругу цвета от красного,
желтого, до синего, фиолетового. На средней
иллюстрации от центра к
краю, увеличивается насыщенность цвета .
Изменение яркости от более
темного у основания до белого у
вершины - правая иллюстрация. Все три
значения любого цвета могут быть
измерены специальным инструментом -
спектрофотометром. Вы можете легко
изменять изображение, изменяя только
одно из этих значений. Именно
поэтому они часто используются, как
переменные параметры в программном
обеспечении для редактирования
изображений. Множество математических
моделей было
создано, используя эти значения.
Каждая из них присваивает
каждому цвету определенное
значение.
Чтобы Вас не запутать,
здесь представлены только две аппаратно-независимых модели : В
1931 году была разработана
модель Цвета xyz, также называемая
модель Цвета Нормы
Международной Комиссией по Освещению (МКО)
{Internationale d'Eclairage (CIE)}. МКО определяет стандарты для
работы с цветом и освещением. На
иллюстрации изображена схема их
Колориметрической системы Нормы (Norm
Color system), еще называемой пространством XYZ
(значение цвета располагается в 3-х
мерной Декартовой системе координат -
что позволяет цветовой охват модели
назвать пространством):
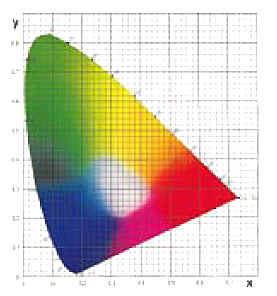
В этой координатной системе
каждый цвет был назначен определенной
точке внутри этого абстрактного
треугольника, охватывающего все
цвета, видимые человеческому глазу. В
ходе длительного эксперимента был
построен график цветового
возбуждения стандартного наблюдателя
при определенном угле зрения и
освещения. По
оси x координатной плоскости Вы видите
красные цвета, в то время как зеленые
цвета расположены по оси z. Этот двухмерный
график показывает все цвета независимо
от их яркости. Если Вы можете вообразить
третью ось y, которая расположена перпендикулярно к плоскости графика,
различные значения яркости лежали бы
здесь. Одна из проблем этой системы, хотя бы, - то, что расстояния
между цветами не соответствуют нашему
восприятию цвета , и что, используется третье
измерение, таким образом яркость,
является трудно определима. В то
же время спектрофотометры для своей
работы используют эту аппаратно-независимую
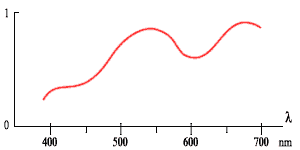
модель описания цвета. Как происходит
измерение :- через
интерференционные фильтры с шагом 2 nm,
происходит замер длин волн, отраженных
от объекта, стоится график
R(![]() ):
):
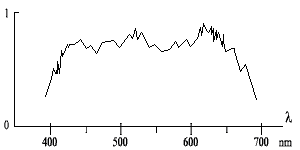
Используя график кривой спектра источника освещения S
(![]() ):
):
И кривые сложения (смешения) цветов стандартного наблюдателя :
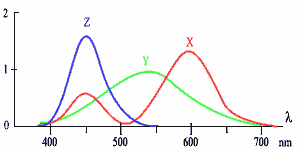
По формулам вычисляются координаты X, Y, Z:
|
X=K* Y=K* Z=K* |
где:- K- коэффициент приведения яркости белого (объекта), к точке белого системы координат. |
В 1976 комиссия разрабатывает
математическую модель - L*a*b*:
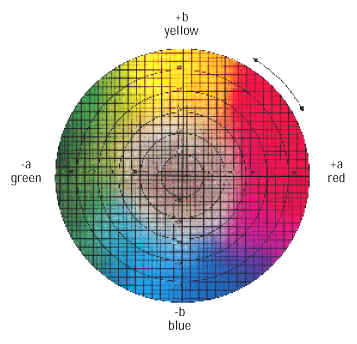
Цветовое пространство L*a*b* представлено в трех размерностях. Все цвета с равной яркостью все еще лежат на одной плоскости модели. Здесь Вы можете видеть, что плоскость имеет две оси - ось слева направо a* ось b* от основания до вершины.
-
L*=116(y/yn)*1/3
-
a*=500*(x/xn*1/3-y/yn*1/3)
-
b*=500*(z/zn*1/3-Y/Yn*1/3) где: x, y,z -координаты точки белого; xn,yn,zn -координаты точки нужного цвета.
Внешний периметр цветового круга несет цвета - красный и зеленый, желтый и синий,- противоположные цвета - цвета находящиеся друг напротив друга: противоположный красному - зеленый, противоположный синему - желтый. Перемещаясь от центра , по оси а* оценивается местоположение цвета относительно оси красный-зеленый. Ось b* оценивает местоположение цвета относительно оси синий-желтый. Яркость, увеличивается от основания модели к вершине. Трехмерная цветовая модель L*a*b*:
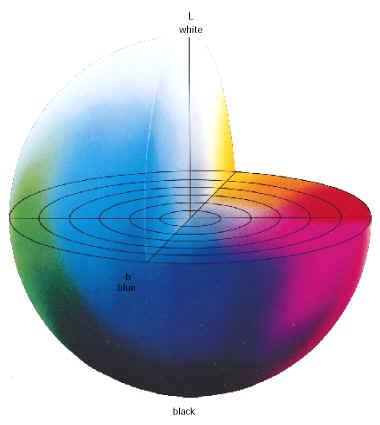
Вы можете назвать каждый цвет
точно, задавая значения яркости, и
величины смещения по осям a* и b*.
В реальном мире, тем не менее,
это не очень удобно,
представьте, что Вы заказываете галстук цвета: L* = + 43.51, a* = + 15.45, и b* = - 22.85. Но в цифровом мире аппаратно независимая модель
представления цвета необходимость в
частности как промежуточное цветовое
пространство при переводе цвета из
одного аппаратно-зависимого
пространства в другое. Используя L*a*b*
в программе Photoshop, обратите внимание, что Adobe выбрала D50, twodegree observer
L*a*b*, 2 гр.
И Вам, снимая показания L*a*b* с помощью спектрофотометра, следует выбрать его же.
